These hard math problems are so tricky they'll give your brain a workout

17 Hard Math Problems That’ll Make Your Head Spin

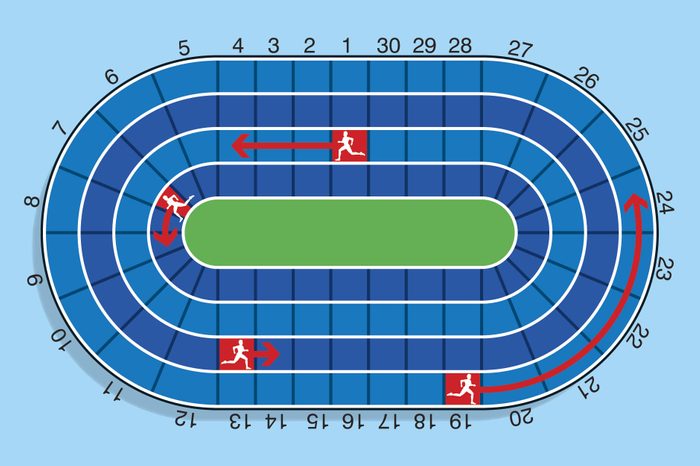
Track and field
If each of these runners travels the indicated number of spaces in the same amount of time, at which numbered spot will all of the runners be next to one another?
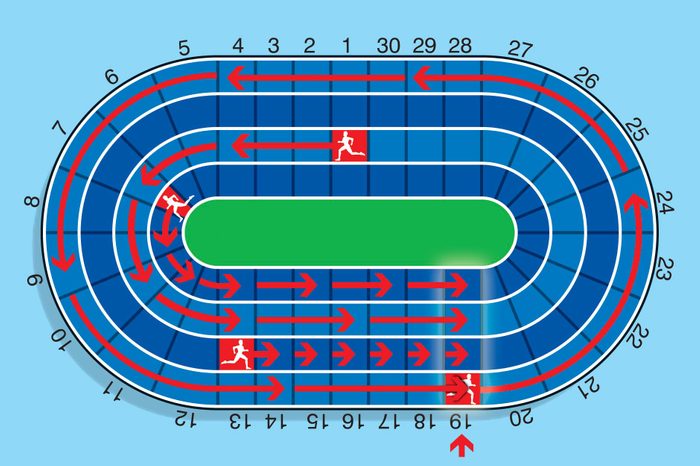
Answer: Space 19
At first, it seems like this brain teaser will take forever to figure out—but, in actuality, the runners will all be lined up after only six “moves.” Make a chart indicating where each runner will be after each move. To figure that out, all you really need to do is add! Just add the number of spaces each runner advances—three, two, one, and five—to the number they’re already at, going back to Space 1 after 30. Sure enough, they’ll all reach Space 19 at the same time.

Ones and zeros
In this slide, you’ll see the binary notation for the numbers 1 through 7. (Binary notation means the number is represented by ones and zeros.) Following the pattern, what is the binary notation for the number 12?

Answer: 1100
What makes this brain game more difficult than most hard math problems is that it’s so unlike how we’re used to looking at numbers, especially in a sequence. In the base-10 system (aka decimal system) we’re used to, the first digit on the right represents the number of ones, the second digit represents the numbers of tens, and the third digit represents the number of 100s.
But in the binary system, the first digit on the right represents the number of ones, the second digit represents the number of twos, the third digit represents the number of fours and the fourth digit represents the number of eights. So to make 12, grab an eight (the fourth digit) and a four (the third digit) and just write them with 1s in those spaces: 1100.

Face value
Which number should be on the bottom right stamp? (Hint: It’s a one-digit number.)

Answer: 1
Many of these hard math problems are more about identifying relationships between groups of numbers than doing any actual hard math. In this case, don’t look at the horizontal rows of stamps but at the vertical pairs of stamps. Each pair of vertical stamps is a simple division operation.
The number in the tens place of the top stamp, divided by the number in the ones place of the top stamp, equals the number on the bottom stamp. So, for the first pair, 8 divided by 2 is 4. In the last pair, 2 divided by 2 is 1.

Energy saver
A transport company is greatly reducing the amount of oil it uses—but by how much? What number should be below the final barrel?

Answer: 2
This tricky math problem doesn’t require arithmetic at all! It’s all about noticing patterns. (Thank goodness, because those are some wacky large numbers that would not be fun to compute.) Take a look at the first and second oil barrels, and notice that they share four numbers. But how are they different? The second is shorter, missing the 1, and the reverse of the remaining numbers from the first barrel.
Now look at the second and third barrels. Those also share numbers, minus the first one (7). Are you seeing the pattern? Each successive barrel removes the first digit and reverses the remaining numbers. So, what’s the last barrel’s number? When you remove the first digit from the second barrel (4), you’re left with just 2. No need to reverse a number with only one digit, so there’s your answer.
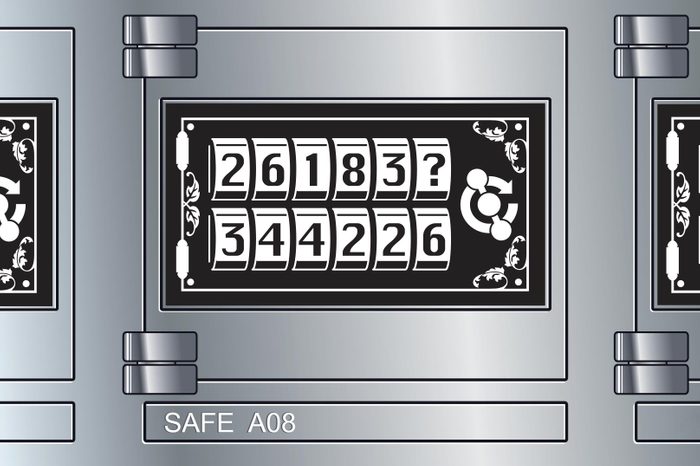
Safe code
What’s the digit you need to input in the space with the question mark to complete the code for the safe? Here’s a hint to save you some stress: The “Safe A08” text on the bottom is meaningless, so don’t waste time trying to figure out if that will help you get the answer!
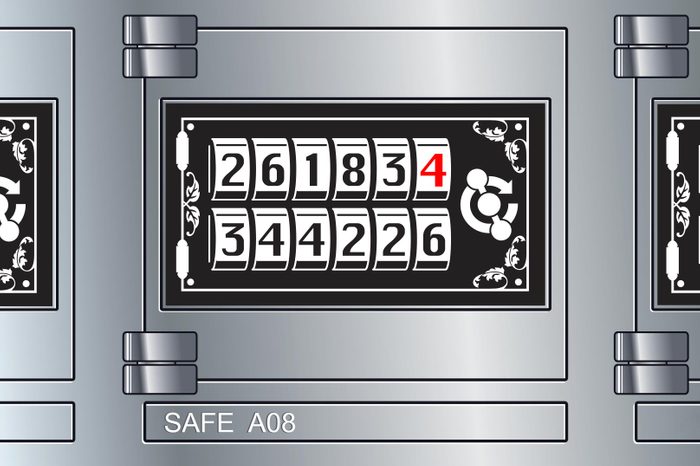
Answer: 4
To figure this one out, it helps to remember that rows of numbers aren’t always a sequence in their own right. They can also be groups of numbers written together. That’s what’s happening here: Like the Abraham Lincoln stamps puzzler, this safe has three vertical pairs of two-digit numbers: 26 and 34, 18 and 42, and thirty-something and 26.
So what’s the pattern? For each vertical pair, the number on the top left is multiplied by 2 to get the number on the bottom right, and the number on the bottom left is multiplied by 2 to get the number on the top right. For example, if we look at the first vertical pair, 2 times 2 is 4 and 3 times 2 is 6. So to get the missing number in the last pair, multiply 2 times 2, which gives us 4 as the answer.

Symbol sums
For this one, you need to figure out which mathematical symbols—add (+), subtract (-), multiply (x), divide (÷)—go in the boxes to make the math equation work. Here’s one tip: The proper order of operations doesn’t apply, so you can just work the problem from left to right.

Answer: – , + , ÷
Here is the correct equation: 21 – 3 + 18 ÷ 6 = 6.

Rack ’em
Put the billiard balls into their correct spots of corresponding colors so that the sum of every column, row and diagonal is 49.

Answer:
Sometimes hard math problems are just about trial and error, and eliminating possibilities that don’t work—kind of like Sudoku. But there’s often a little bit of strategy involved. Take the three diagonal yellow balls that are filled in for you. That’s a great place to start, since you only need one ball (a yellow No. 1) to add up to 49.
For the leftmost column and the bottommost row, you already have a number that ends in 3, so you’ll need the sum of the other three numbers to end in 6. And you also know that you can’t put the 25 ball or the 31 ball in any row, column or diagonal with the 23 ball because they’d immediately make your sum too big. After that, it’s just working out the math.

Number music
For this math exercise, see how fast you can solve these not-so-hard math problems while blasting your favorite music. Oh—and try not to use a calculator!

Answers:
Most of these are just simple arithmetic, or even common knowledge that you picked up in elementary school. For the more complicated ones, remember the order of operations. In other words, do multiplication and division before you do addition and subtraction.

Do the math
For this one, fill in the numbers 1 through 9, using each only once, to make all of the vertical and horizontal equations correct.

Answers:
Here’s another one that probably just takes some time and several incorrect guesses.

Strike
Which pins do you have to knock over to get a total of 100 points?

Answer: 13, 39, and 48
This one is tricky because it doesn’t tell you how many pins you need to knock over, so it could be any combination of the pins. But that’s the only combo that adds up to exactly 100!

Maximize
Using only numbers 1 through 9 with no repeats, replace the three question marks to make the answer the largest number possible.

Answer:
The largest possible solution for this math problem is 44418, and to yield that result, you need to add 128 to 79894, and then subtract 35604. Say what now? Here’s how it works. You want the first two numbers to be as large as possible, and the third number to be as small as possible, so that when you subtract the bottom number from the sum of the top two your answer will qualify as the “largest possible solution.”
To make that happen, use 8 and 9 in the top numbers, and it matters which one goes where: 128 + 79,894 is larger than 129 + 78,894. Then, use the smallest number (0) in the bottom number. Though this problem might seem mind-boggling at first, the answers really do make sense; you want to get the largest possible sum and then subtract the smallest possible number from it.

Diary time
What time is the last appointment?

Answer: 19.50
For this answer, you’ll quickly notice a pattern if you add up the digits in each time; ignore the decimal points. The digits in the first “time” add up to 11; the second, 12; the third, 13; and, well, you’ve now got a seriously simple pattern. So you know that the digits in the fifth time must add up to 15. And when you add them … they already do! So the question mark must be replaced with a 0 to keep the sum at 15.

Same same
Using math symbols—add (+), subtract (–), multiply (×), divide (÷), square root (√)—can you make all of these equations true? The symbols don’t just have to be where the ellipses are; they can be before the first number too (though there won’t be any negative numbers). And there can be more than one symbol in each ellipsis spot. Finally, you’re allowed to group pairs of operations together with parenthesis.

Answers:
OK, yeah, that might have been the hardest of these hard math problems! Square roots can make things extra confusing, and it takes some serious brainpower and ingenuity to figure out where to place those parentheses.
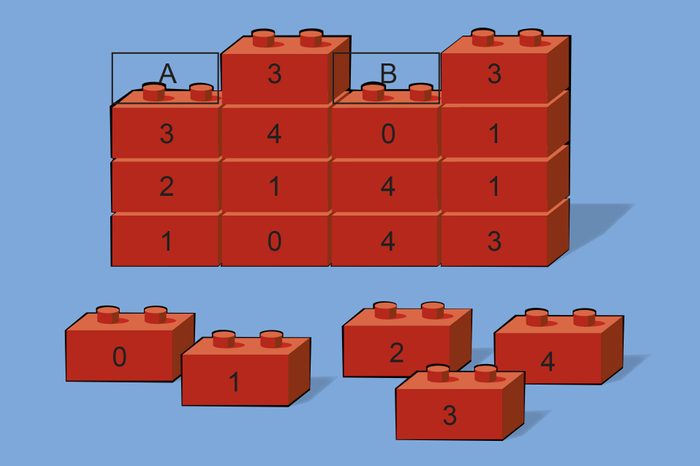
Build it
Which blocks should go in Space A and Space B?

Answer: Block 2 in Space A and Block 0 in Space B
This is one of the slightly easier of these hard math problems (and a nice break after that last one, frankly)! You might notice that all of the complete horizontal rows and complete vertical columns add up to 8. If you did, you know exactly which numbers will make the incomplete rows equal 8, too.
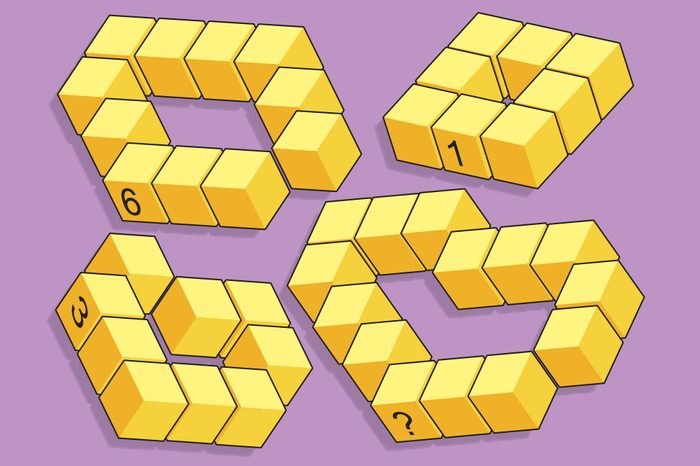
Number blocks
What number should replace the question mark on the bottom right loop?
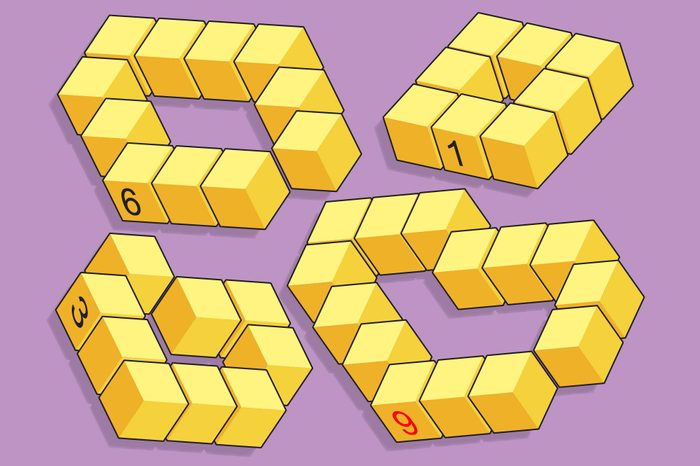
Answer: 9
And we’re back to a really tricky one! The number on each loop is the number of blocks that could fit in the middle.
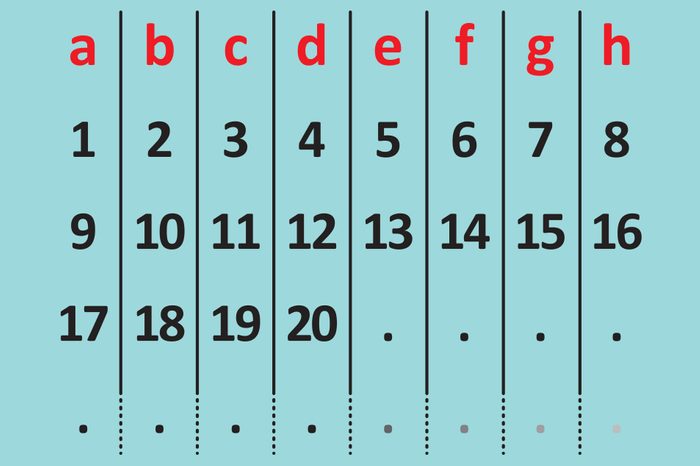
Place 100
Without writing out every single number, can you figure out which letter the number 100 will be underneath?
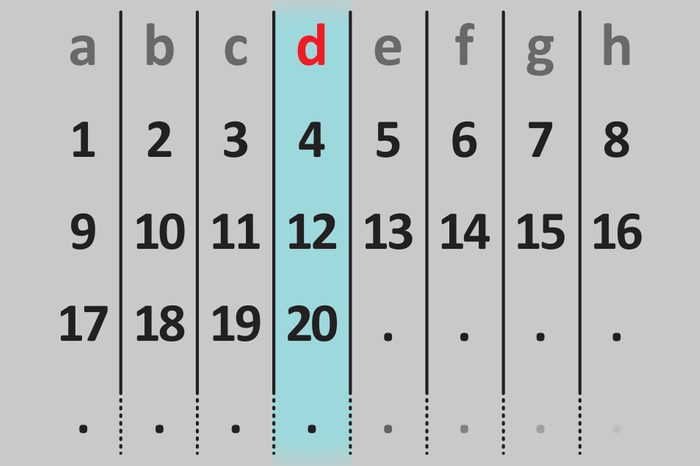
Answer: Letter d
Since 100 is a multiple of 10, the way to solve this is to figure out where each multiple of 10 will land. First, notice there are eight columns. So, after eight numbers, a new row starts with the letter “a” again. Therefore, each multiple of 10 will be two “letters” after the previous multiple of ten. In the table, you can already see that 10 is under the letter “b” and 20 is under the letter “d.” So 30 will be under “f,” 40 will be under “h,” 50 will circle back to “b” and so on.

It’s a sign
What number should go on the bottom right sign?

Answer: 11
For this one, all you’re doing is putting minus signs between the top and second signs and between the second and third signs, and then an equal sign between the third and bottom signs. So you’re subtracting, and then subtracting again, to get the bottom numbers. So in the first column, you do 41 – 17 – 14 to get 10. In the final column, you subtract 21 from 37, and then subtract 5 from that, to get the missing number, 11.
FAQ
What is the hardest math problem?
Well, first of all, there isn’t just one hardest math problem, but seven of them! In 2000, the Clay Mathematics Institute of Cambridge, Massachusetts, laid out seven “Millenium Problems,” each with a $1 million prize. Only one, the Poincaré Conjecture, has been solved so far, leaving six juicy conundrums for mathematicians of the future. One of the problems, the Riemann hypothesis, has been waiting to be solved since 1859!
What is the answer to this math problem: x3+y3+z3=k?
Known as the “sum of cubes” problem, the catch is that for any value of k, the values of x, y and z must be whole numbers, which also includes negative numbers. For instance, if k is 3, the values of 1, 1, and 1 work for x, y, and z, but so do 4, 4, and -5. It turns out that as k goes from 1 to 100, it quickly becomes very difficult to calculate what values of x, y and z are needed to make the equation work, requiring the aid of computers to manipulate numbers 20 or more digits long. When mathematicians come up with new solutions for a value of k, it’s such a big deal that they publish a paper to announce the result!
What is the real answer to 6 ÷ 2 (1+2)?
A few years ago the internet went crazy over this math problem: 6 ÷ 2 (1+2). Depending on the order in which you do the operations, you get either 1 or 9, and there was fierce debate over which order was correct. Everyone agrees about one thing: First, you add 1 and 2 in the parentheses to get 3. This gives you an equation that reads 6 ÷ 2 (3). The second part of the equation tells us to multiply 2 by 3, so many people argued that the equation reduced to 6 ÷ 6 or 1. But order of operations tells us to divide or multiply in order from left to right, which would have us take care of 6 ÷ 2 first to get 3, and then multiply 3 by 3 to get 9, the correct answer.
Sources:
- Khan Academy: “Binary Numbers”
- Clay Mathematics Institute: “The Millenium Prize Problems”
- Slate: “What Is the Answer to That Stupid Math Problem on Facebook?”
- MIT News: “After cracking the “sum of cubes” puzzle for 42, mathematicians discover a new solution for 3”


















